what is a complex number?
complex number definition is that numbers that consist of both a real part and an imaginary part. They are represented as a + bi, where ‘a’ is the real part, ‘b’ is the imaginary part, and ‘i’ is the imaginary unit (√(-1)). Complex numbers are essential in various fields, including mathematics, engineering, physics, and signal processing.
To solve a complex number problem, follow these steps:
Addition and Subtraction: Add or subtract the real and imaginary parts separately.
Multiplication:
Use the FOIL method to distribute and combine like terms.
Division:
Multiply the numerator and denominator by the complex conjugate of the denominator to eliminate the imaginary part.
Finding the Conjugate:
The conjugate of a complex number a + bi is a – bi, where ‘a’ and ‘b’ are real numbers.
Complex number calculator also have various properties, such as commutativity, associativity, distributivity, and the existence of additive and multiplicative identities. Understanding these properties is crucial for effectively solving complex number problems.
Here are some common types of complex number problems:
Addition and Subtraction: Perform addition and subtraction operations between complex numbers by separately combining their real and imaginary parts.
Multiplication and Division: Multiply and divide complex numbers using the distributive property and i^2 = -1.
Conjugates: Find the conjugate of a complex number, which is obtained by changing the sign of the imaginary part.
Modulus: Calculate a complex number’s modulus (or magnitude), which represents its distance from the origin in the complex plane.
Argument: Determine the argument of a complex number, which represents the angle it makes with the positive real axis in the complex plane.
Powers and Roots: Raise complex numbers to powers and find their roots using De Moivre’s theorem.
Solving Equations: Solve complex number equations like quadratic equations involving complex coefficients or variables.
Graphing: Represent complex numbers in the complex plane and understand their geometric interpretation.
Complex number problems find applications in various fields, including electrical engineering, signal processing, physics, computer graphics, and quantum mechanics. Mastering complex number operations is essential for solving advanced mathematical problems and real-world applications in these disciplines.
Solution:
This problem involves determining the absolute value of the complex number expression. With detailed explanations, we have demonstrated step-by-step methods for tackling this. Each root must be represented in terms of w and w square, which is the most challenging part of the problem. We use the properties of w and w square to complete the solution. For a clear understanding, they are explained in detail. Solving these problems becomes much easier after you learn the method.
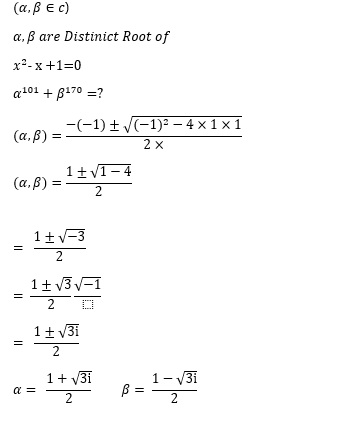
For a complete solution watch the above vide:
Application of cube root of unity:
The cube root of unity has various applications in mathematics, physics, engineering, and signal processing. Some of its key applications include:
Solving Equations: The cube root of unity, denoted as ω, is a complex number that satisfies the equation ω^3 = 1. It is used to find solutions to cubic equations and related problems in algebra.
Complex Number Operations: Cube roots of unity play a crucial role in complex number arithmetic, especially in finding the roots of complex polynomials and solving complex equations.
Fourier Transforms: In signal processing, the cube roots of unity are used in the discrete Fourier transform (DFT) to decompose signals into their frequency components.
Rotation in 2D Space: The cube roots of unity are used to represent rotations in a 2D plane, making them valuable in computer graphics and geometry.
Group Theory: The set of cube roots of unity forms a cyclic group under multiplication, which has important applications in group theory and abstract algebra.
Quantum Mechanics: In quantum mechanics, the cube roots of unity are used in the mathematical representation of quantum states and operations.
Trigonometric Identities: The cube roots of unity are used to derive trigonometric identities and simplify trigonometric expressions.
Overall, the cube root of unity is a fundamental concept in mathematics, and its applications extend to various fields, making it an important topic of study in advanced mathematics and beyond.



