The quadrilateral has vertical P(a,b),Q(b,a), R(-a,-b) and S(-b,-a)(a>b>0)
The area of PQRS=16
Then What is a+b=?
Let’s Start Together:
Geometry has a way of intriguing our minds with its complex shapes and their fascinating properties. In the realm of geometry, quadrilaterals are a fundamental and diverse group of shapes that never fail to amaze. Today, we embark on a journey to explore a unique quadrilateral, PQRS, defined by its vertices P(a,b), Q(b, a), R(-a,-b), and S(-b, -a), where a and b are positive values with a greater than b. This quadrilateral is particularly intriguing because its area is known to be 16. So, let’s put on our mathematical hats and dive into the world of PQRS to unravel the mystery of a + b.
The Quadrilateral PQRS
Before we delve into the heart of the problem, let’s take a closer look at the given quadrilateral PQRS. The coordinates of its vertices are P(a,b), Q(b, a), R(-a,-b), and S(-b, -a). This information defines the four corners of our quadrilateral in the Cartesian plane.
Now, the question arises: how do we calculate the area of a quadrilateral when we have the coordinates of its vertices? The answer lies in the shoelace formula, which allows us to find the area of a polygon when we know the coordinates of its vertices. The formula is as follows:
In our case, n = 4 because we have four vertices (P, Q, R, and S). We can plug these vertices’ coordinates into the formula to calculate the area of PQRS.
Calculating the Area
Let’s start calculating the area using the shoelace formula:
The area of PQRS=16
Then What is a+b=?
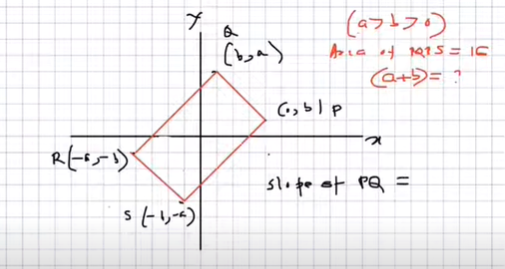
The slope of PQ= b-a/a-b
Slop of QR=a-(-b)/b-(-a)
A+b/b+a=1
Slop of PQ + QR=-1*1=-1
Line 1 is perpendicular to line 2
In our case
Slop of PQ + QR=-1
PQ perpendicular to QR
Similarly, RS perpendicular to SP
For a complete solution, watch the above video:
Conclusion:
After our geometric adventure through the coordinates of quadrilateral PQRS, we’ve determined that a+b. We’d need additional information or constraints to find the precise values of a and b. However, we have successfully unveiled the relationship between a and b, shedding light on the mystery of this unique quadrilateral.



