The Ratio of the area is a fundamental mathematical concept used to compare the sizes of two-dimensional figures, particularly the areas enclosed by these figures. It helps us understand how one area relates to another and is commonly used in geometry, mathematics, and various real-world applications.
The Formula for Area of Shapes
Before delving into the Ratio of area, it’s essential to understand the formula for calculating the area of common shapes. For example, the area of a rectangle is given by length × width, the area of a triangle is calculated as 0.5 × base × height, and the area of a circle is π × radius².
Calculating the Ratio of Area
To calculate the Ratio of area between two shapes, you need the areas of both shapes. Let’s consider two shapes, Shape A and Shape B, with areas A and B, respectively. The Ratio of their areas (A to B) is given by:
The Ratio of Area = Area of Shape A / Area of Shape B
Interpreting the Ratio
The Ratio of the area provides valuable information about how one area compares to another. It’s important to note that the Ratio is a dimensionless quantity, meaning it has no units. The Ratio can be expressed as a fraction, a decimal, or x: y depending on the context.
Application in Geometry
In geometry, the Ratio of the area is frequently used to compare similar figures. For example, when you have two similar triangles, the Ratio of their areas is the square of the Ratio of their corresponding sides. This property holds for other similar shapes as well.
Real-World Examples
The concept of the Ratio of the area finds applications in various fields, such as architecture, engineering, and art. Architects use it to determine the optimal use of space, while engineers use it to assess the load-bearing capacity of structures. In art, understanding the Ratio of the area can lead to visually appealing compositions.
The Ratio of the Area of a Larger Circle to a Smaller Circle:
Calculating the Ratio of the areas of a larger circle to a smaller circle involves a simple geometric relationship that can be expressed using the formula for the area of a circle. The area of a circle is given by the formula A = πr², where “r” represents the circle’s radius. When comparing the areas of two circles, we can use this formula to find the Ratio between them.
Let’s say we have a larger circle with a radius of R and a smaller circle with a radius of r, where R > r. The Ratio of their areas (larger to smaller) can be calculated as follows:
Ratio = Area of Larger Circle / Area of Smaller Circle
Ratio = πR² / πr² Ratio
= (R²) / (r²)
= (R/r) ²
This Ratio provides insight into how much larger the area of the larger circle is compared to the smaller circle.
Now we have two diagrams:
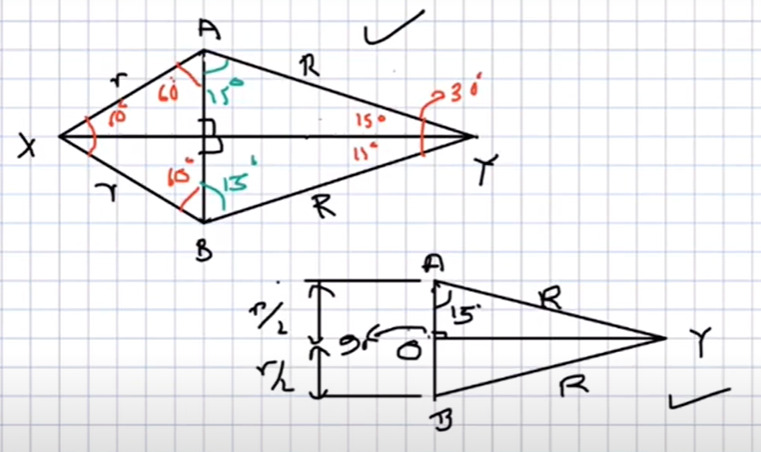
In the first Diagram:
<AxA=60
xA=xB=r
Hence
<xAB=<xBA=120/2=60
Hence,
Ao=oB=AB/2=r/2
In the second diagram
<oAY
=180-90-15
=75
Ao/AY=Cos75
=(r/2R) =Cos75
= we can write 75 (r/2R)= Cos(45+30)
(r/2R) = Cos45 Cos30 -Sin45 Sin30
Now, use their values
To check the complete solution, click here to check the complete video
In real-world applications, this concept is useful when comparing the size or capacity of circular objects. Whether you’re working with circles in geometry, considering proportions, or evaluating the relationship between areas, the Ratio of areas provides a simple and effective tool for analysis.
Conclusion
The Ratio of the area is a versatile mathematical tool that allows us to compare the sizes of shapes and understand their relationships. It’s a fundamental concept with wide-ranging applications in both theoretical and practical domains. By calculating and interpreting the Ratio of area, we gain insights into the relative magnitudes of different two-dimensional figures.



