Geometry has a fascinating way of revealing relationships between shapes, and one intriguing problem involves finding the difference in areas between a circle and a triangle. Specifically, we want to understand the areas of regions that lie on the circle but outside the triangle and the area of the triangle that extends beyond the circle’s boundaries. This blog post will walk you through the steps to tackle this geometric challenge. By the end, you’ll clearly understand how to calculate these differences and gain insight into the interplay of these two fundamental shapes.
Step 1: Identify the Circle and Triangle: Identify the two main shapes at play—the circle and the triangle. You should know the circle’s radius and the triangle’s dimensions, such as its base and height.
Step 2: Calculate the Area of the Circle: The first task is to calculate the area of the entire circle. This can be done using the formula A_c = π * r^2, where “r” represents the circle’s radius.
Step 3: Calculate the Area of the Triangle: Next, find the area of the entire triangle using the formula A_t = (1/2) * base * height, where “base” is the length of the triangle’s base and “height” is the perpendicular distance from the base to the opposite vertex.
Step 4: Determine the Areas of Interest: To find the difference in areas, we need to isolate the regions of interest:
· Area 1 represents the portion of the circle that lies outside the triangle. Calculate this by subtracting the triangle’s area from the circle’s area: Area 1 = A_c – A_t.
· Area 2 represents the triangle section extending beyond the circle’s boundaries. Calculate this by subtracting the circle’s area from the triangle’s area: Area 2 = A_t – A_c.
Step 5: Calculate the Differences: Now, you have two values—Area 1 and Area 2—representing the differences in areas between the circle and the triangle. These values give insight into how much of each shape lies outside the other.
Solution
Find the difference between areas of regions that lie on the circle but outside the triangle and the area of the region of the triangle that lies outside the circle.
We have shaded the area which we need to calculate:
The area of the circle
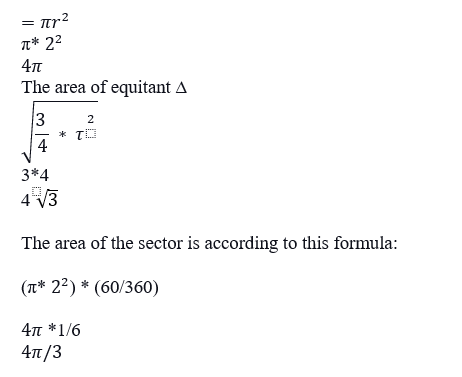
Now, the area of the circle that lies inside of the circle but outside equilateral ∆
That is blue shaded area that comes to
For a complete solution, watch above
Conclusion:
Geometry offers us the tools to explore the relationships between shapes, and this problem of finding the difference in areas between a circle and a triangle is a prime example. You can calculate the areas of interest by following the steps outlined in this blog post. These regions lie on the circle but outside the triangle and the area of the triangle that extends beyond the circle. This mathematical exercise deepens your understanding of geometry and showcases the elegance of these fundamental shapes in action. So, put your newfound knowledge to the test in your next geometric adventure!



