To find the area of the congruent side of an isosceles triangle, you’ll first need to understand some key properties of isosceles triangles and then apply the appropriate formula. An isosceles triangle has two sides of equal length and two equal angles. Let’s go through the steps to find the area of the congruent side:
1. Identify the Isosceles Triangle: Identify the isosceles triangle in question. You should have information about the lengths of the two equal sides (often referred to as legs) and the measure of the included angle (the angle between the two equal sides).
2. Determine the Length of the Congruent Side: The congruent side, which is not one of the legs, is the triangle’s base. You may need to use properties of isosceles triangles or given measurements to find its length.
3. Calculate the Height of the Triangle: To calculate the area of a triangle, you need the height (h) and the base (b). In this case, the congruent side serves as the base. The height is the perpendicular distance from the base to the opposite vertex. You may use various methods to find the height depending on the information given.
4. Apply the Area Formula: The formula for the area of a triangle is:
Area (A) = 0.5 * base (b) * height (h)
Substitute the values you found for the base and height into this formula.
5. Calculate the Area: Plug in the values for the base and height into the formula and calculate the area.
Here’s a summary of the steps in a more concise form:
1. Identify the isosceles triangle.
2. Determine the length of the congruent side (base).
3. Calculate the height using the properties of the triangle.
4. Use the area formula: A = 0.5 * base * height.
5. Calculate the area.
Remember that the area of the congruent side (base) depends on the specific information given for the triangle. If you have the lengths of the legs and the included angle, you can often use trigonometric functions (such as the sine or cosine) to find the height and, subsequently, the area of the congruent side.
Reasons for Its Importance:
Finding the area of the congruent side of an isosceles triangle is important for various reasons, both in theoretical mathematics and practical applications. Here are several reasons why determining the area of the congruent side of an isosceles triangle holds significance:
1. Geometric Understanding: Calculating the area of the congruent side of an isosceles triangle helps develop a deeper understanding of geometric properties and relationships. It reinforces the concept that the area of a triangle depends on its base and height, and this knowledge can also be extended to other types of triangles.
2. Mathematical Problem Solving: It provides practice in solving mathematical problems and applying geometric principles. This skill is valuable in mathematics and various STEM (science, technology, engineering, and mathematics) fields where geometry and trigonometry are used extensively.
3. Architectural and Engineering Applications: In architecture and engineering, understanding the area of triangles, including isosceles triangles, is crucial for designing structures, calculating surface areas, and determining materials required for construction.
4. Surveying and Land Measurement: In surveying and land measurement, triangles are often used to estimate distances and areas of irregularly shaped plots of land. Knowing how to calculate the area of an isosceles triangle helps in accurate land assessment.
5. Art and Design: Artists and designers use geometric shapes. Calculating the area of isosceles triangles can be useful for creating visually appealing compositions and patterns in art and design.
6. Scientific Analysis: In scientific research, particularly in physics and biology, geometric concepts are used to model and analyze various phenomena. Calculating areas, including those of isosceles triangles, can aid in data interpretation and analysis.
7. Problem Solving in Everyday Life: Beyond formal applications, understanding the area of isosceles triangles can be useful in everyday situations. For instance, it can help with tasks like determining the amount of space covered by a roof or calculating the area of a piece of land.
8. Educational Foundation: Teaching and learning about isosceles triangles and their areas are fundamental components of geometry education. These concepts serve as building blocks for more advanced mathematical topics.
9. Problem Variability: Isosceles triangles come in various sizes and configurations, making them a versatile tool for teaching and problem-solving. Calculating the area of the congruent side allows students and professionals to work with triangles of different dimensions and angles.
Solution
Length of the two congruent sides of the isosceles triangle:
The formula of the area of the equal letter
∆ABC=
area of the equal letter ∆
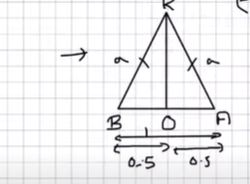
KB=KA=a
BO=OA=1/2=0.5
For a complete solution, watch the above video:
Conclusion
In essence, understanding how to calculate the area of the congruent side of an isosceles triangle is not only academically significant but also has practical applications that extend into many aspects of our daily lives and professional endeavors. It stands as a testament to the enduring importance of geometry in shaping our understanding of the world around us and our ability to solve complex problems.



