In the world of mathematics, there exists an endless realm of intriguing equations and expressions that can leave even the most seasoned mathematician in awe. Today, we embark on a journey to decipher one such expression, where the α and β roots play a pivotal role. The equation at hand is:
x² + 6x – 2=0
Where α and β are the roots, with α being greater than β. This equation sets the stage for our exploration into an expression involving these roots, particularly when exponentiation comes into play:
(n^a) = α^n-β^n
Our primary goal is to find the value of the given expression:
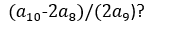
Let’s dive into this captivating mathematical puzzle and uncover its secrets.
Unraveling the Expression:
The expression
na=αn−βn
tells us that for any positive integer n greater than 1, we can calculate na by subtracting the n-th power of β from the n-th power of α. But how does this help us find the value of
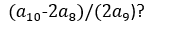
To understand this, let’s break it down step by step.
First, we need to find an, which represents the n-th term of a sequence. We can do this using the formula:
an=αn+βn
With this formula in hand, we can calculate an for n = 8, 9, and 10.
a8=α8+β8
a9=α9+β9
a10=α10+β10
Now, we can substitute these values into the expression:
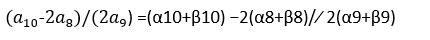
For the complete solution, watch the above video:
Calculating this expression requires some algebraic manipulation, which involves utilizing the properties of α and β. After some algebraic gymnastics, we can eventually arrive at the final value of the expression.
Conclusion:
In the world of mathematics, seemingly complex expressions often hide elegant solutions waiting to be uncovered. The journey to find the value of the expression
a10−2a8/2a9 led us through the exploration of roots α and β, an intriguing sequence formula, and some algebraic manipulation.
While the exact value of the expression would require further mathematical calculation, we have taken a significant step toward unraveling this puzzle. This journey reminds us of the beauty and complexity inherent in mathematical exploration and the satisfaction that comes from solving even the most intricate equations.



