Mathematics is often likened to solving puzzles, and today, we embark on a journey to solve a system of equations that will reveal the values of x and y, allowing us to find the elusive expression x^2 + y^2. Our equations are:
y + 4 = (x – 2)^2
x + 2 = (y – 2)^2
With the stipulation that x ≠ y, we’ll dive deep into these equations, exploring their intricacies to unlock the solution that leads us to the treasure, x^2 + y^2.
Solving the System of Equations:
Our task is to find the values of x and y that satisfy both equations simultaneously. Let’s start by rewriting the equations to make them more manageable:
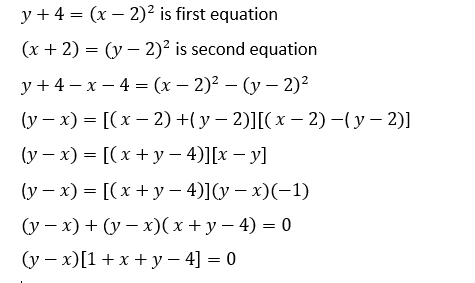
For a complete solution watch the above video:
Conclusion:
Solving a system of equations, especially when it involves nonlinear equations like the ones we encountered in this blog, can be a challenging but rewarding endeavor. In this quest, we started with two equations, y + 4 = (x – 2)^2 and x + 2 = (y – 2)^2, with the constraint that x ≠ y.
By finding the solutions for x and y in this equation, we can finally determine the value of x^2 + y^2. Solving complex equations like these not only tests our mathematical prowess but also deepens our appreciation for the elegance and beauty of mathematics.



