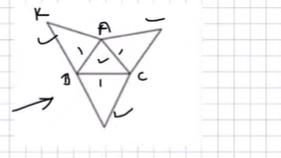
Three congruent isosceles triangles are formed with the base of equilateral triangle of side 1
Sum of the area of this isosceles triangle of the equilateral triangle
Length of one of the two congruent side of the isosceles triangle?
Introduction:
Geometry has always been a fascinating branch of mathematics, and one of the most intriguing shapes in this field is the equilateral triangle. Its unique properties and relationships with other triangles make it a topic worth exploring. In this blog post, we will delve into an interesting geometrical puzzle: What happens when we create three congruent isosceles triangles with the base of an equilateral triangle of side length 1? We will find the length of one of the two congruent sides of the isosceles triangle and calculate the sum of their areas.
The Equilateral Triangle
Before we dive into our problem, let’s refresh our knowledge about equilateral triangles. An equilateral triangle is a special type of triangle in which all three sides are of equal length, and all three angles are congruent, measuring 60 degrees each. It’s like the symphony of triangles, with perfect balance and harmony.
Creating Congruent Isosceles Triangles
Now, let’s set up our scenario. We have an equilateral triangle with a side length of 1. We want to create three congruent isosceles triangles using the base of this equilateral triangle. But first, what exactly is an isosceles triangle?
An isosceles triangle is a triangle with at least two sides of equal length. To make three congruent isosceles triangles with the base of our equilateral triangle, we will split the equilateral triangle into three equal parts by drawing lines from each vertex to the opposite side’s midpoint. This results in three smaller triangles with a base of 1/3 each, as shown below:
Calculating the Area
Now that we have congruent isosceles triangles, let’s calculate their areas. To find the area of a triangle, we use the formula:
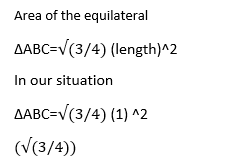
Now let analyze the isosceles triangle
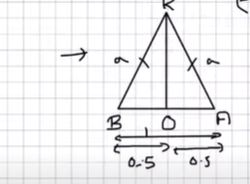
KB=KA=a
BO=OA=1/2=0.5
Now
Kb^2=BO^2+KO^2
A^2=(0.5)^2+KO^2
KO^2=a^2-(1/2)^2
For a complete solution watch the above video:
Conclusion
In this exploration of equilateral triangles and congruent isosceles triangles, we divided an equilateral triangle into three equal parts to create congruent isosceles triangles. We calculated the area of one of these isosceles triangles in terms of the length of one of its congruent sides.
Geometry, as demonstrated here, offers us a fascinating way to dissect and understand complex shapes and their relationships. By solving problems like these, we deepen our knowledge of mathematics and appreciate the beauty of geometric patterns and symmetries that surround us in the world of shapes and figures.



