Quadratic equations are fundamental in mathematics, and they often appear in various scientific and engineering applications. These equations take the form ax^2 + bx + c = 0, where ‘a,’ ‘b,’ and ‘c’ are constants, and ‘x’ represents the variable. The solutions to this equation are the roots, and they play a crucial role in understanding the behavior of the quadratic function. But what happens when one root is the square of the other? In this blog, we’ll explore this intriguing relationship between the roots and delve into the expression b^2 + ca^2 + ac^2 – 3abc, shedding light on its significance in the world of mathematics.
The Roots of a Quadratic Equation:
A quadratic equation can have two real roots, two complex roots, or one real root (a repeated root). The nature of the roots depends on the discriminant, which is given by Δ = b^2 – 4ac.
- If Δ > 0, there are two distinct real roots.
- If Δ = 0, there is one real root (repeated).
- If Δ < 0, there are two complex roots.
One Root as the Square of the Other: Now, let’s consider the intriguing scenario where one root is the square of the other. Mathematically, we can express this relationship as:
r = s^2
This means that if ‘s’ is one of the roots, ‘r’ is the other root, and it’s the square of ‘s.’ This relationship leads to a fascinating result involving the coefficients ‘a,’ ‘b,’ and ‘c’ of the quadratic equation.
The Expression b^2 + ca^2 + ac^2 – 3abc: We are interested in finding the value of the expression b^2 + ca^2 + ac^2 – 3abc in this special case. To do so, we’ll use Vieta’s formulas, which relate the coefficients of the quadratic equation to its roots.
The sum of the roots (r + s) is equal to the negation of the coefficient of the linear term (b/a):
r + s = -b/a
The product of the roots (rs) is equal to the constant term divided by the leading coefficient (c/a):
rs = c/a
Solution:
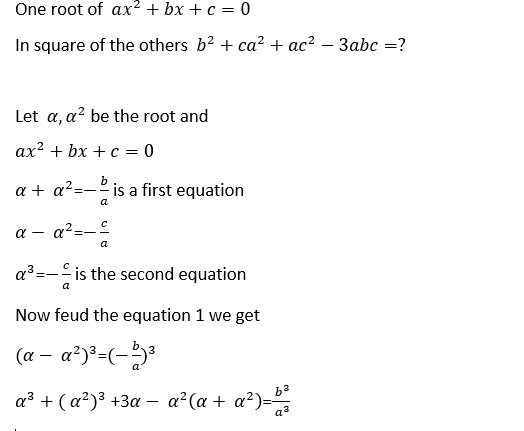
For a complete solution, watch the above Video:
Conclusion:
In this exploration of the relationship between the roots of a quadratic equation where one root is the square of the other, we’ve discovered a fascinating expression involving the coefficients ‘a,’ ‘b,’ and ‘c.’ This expression, b^2 + ca^2 + ac^2 – 3abc, can be derived using Vieta’s formulas and provides insights into the interplay between the roots and the coefficients of the equation. It’s a testament to the richness and complexity of mathematics, where even seemingly simple equations can reveal intriguing patterns and relationships when examined closely.



