When dealing with circles, chords are segments that connect two points on the circumference. Often, we encounter situations where we need to find the length of a chord within a circle, particularly when comparing it to another chord. Let’s delve into finding the length of the larger chord and understanding the key concepts involved.
Understanding Chords in Circles:
Chords are important geometric elements within circles. They can be of varying lengths, and their length often depends on the position of the endpoints on the circle’s circumference. The distance between the two endpoints of a chord is crucial in determining its length.
Identifying the Larger Chord:
To find the length of the larger chord, you need to compare it to another chord within the same circle. Begin by measuring the lengths of both chords. The larger chord will have a greater length between its endpoints. This comparison helps you identify which chord you’re considering in your calculations.
Applying the Chord Length Formula:
The length of a chord can be calculated using a straightforward formula involving the radius of the circle and the central angle subtended by the chord. The formula is:
Chord Length = 2 * Radius * sin(θ/2)
Where:
Radius is the distance from the circle’s center to any point on its circumference.
θ is the central angle (in radians) subtended by the chord at the circle’s center.
Finding the Central Angle:
To calculate the length of a chord, you’ll need to determine the central angle that the chord subtends at the center of the circle. This angle plays a pivotal role in the chord length formula. Use trigonometric principles, such as the inverse sine function, to find the central angle based on the information.
Calculating the Chord Length:
Once you have the value of the central angle, plug it into the chord length formula to calculate the length of the chord. If you’re comparing two chords, repeat this process for both chords to find their respective lengths.
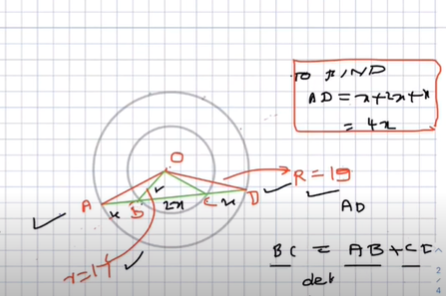
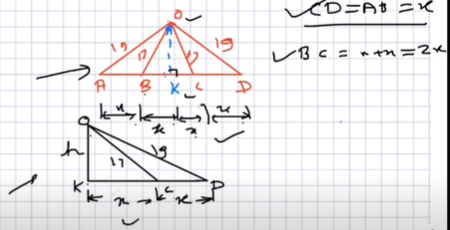
Solution
R=19, r=17
Half of Chord of larger circle lies on smaller circle.
Length of Larger Chord?
Here we have two images:

To get the complete solution, Click Here.
Conclusion:
Finding the length of the larger chord in a circle involves understanding the concepts of chords, central angles, and trigonometric functions. By comparing the lengths of two chords and using the chord length formula, you can accurately determine the length of the larger chord and explore geometric relationships within circles.



